How Many Sides Does a Polygon Have? Unveil the Mystery!
A polygon has multiple sides. It is a closed figure with three or more straight sides.
Polygons are geometric figures that consist of line segments connected at their endpoints. They are two-dimensional shapes and can have any number of sides, as long as they are straight and do not intersect. The simplest polygon is a triangle, which has three sides.
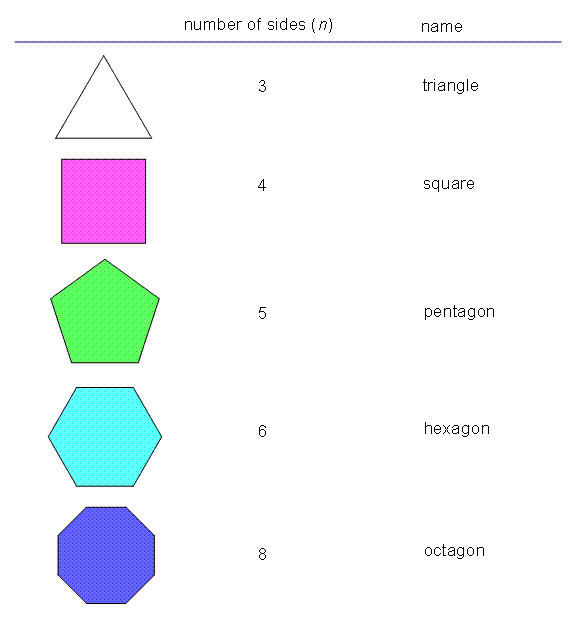
Other common polygons include quadrilaterals (four sides), pentagons (five sides), hexagons (six sides), and so on. The number of sides in a polygon determines its name. For example, a polygon with eight sides is called an octagon. Understanding the concept of polygons and the number of sides they have is fundamental in geometry and can be helpful in various mathematical and real-world applications.
The Basics Of Polygons
Polygons are closed shapes with straight sides. The number of sides in a polygon can vary, from a minimum of three sides in a triangle to an infinite number of sides in a circle. Each polygon has a unique number of sides, which determines its classification.
Defining Polygons
In geometry, a polygon is a closed shape with straight sides.
From Triangles To Nonagons
Polygons can range from 3 sides to 9 sides or more.
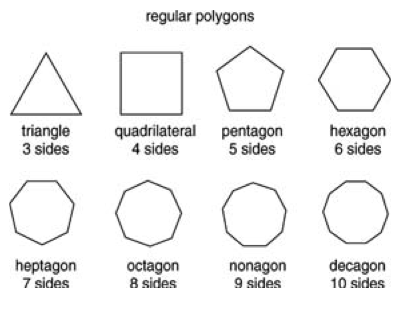
Credit: socratic.org
Categories Of Polygons
A polygon is a closed shape with straight sides. There are different types of polygons based on their sides and angles. The categories of polygons are Regular vs Irregular and Simple vs Complex.
Regular Vs Irregular
Regular polygons have equal sides and angles, while irregular polygons have sides and angles of different lengths and measures. For example, a regular pentagon has five equal sides and five equal angles, whereas an irregular pentagon may have five sides of different lengths and five angles of different measures.
Simple Vs Complex
Simple polygons do not intersect themselves, whereas complex polygons have intersecting sides. A triangle is a simple polygon, while a star-shaped polygon is a complex polygon.
| Regular Polygons | Irregular Polygons |
|---|---|
| – Square | – Trapezoid |
| – Equilateral Triangle | – Pentagon |
| – Hexagon | – Heptagon |
- Regular polygons have equal sides and angles
- Irregular polygons have sides and angles of different lengths and measures
- Simple polygons do not intersect themselves
- Complex polygons have intersecting sides
- Regular polygons have equal sides and angles
- Irregular polygons have sides and angles of different lengths and measures
- Simple polygons do not intersect themselves
- Complex polygons have intersecting sides
In conclusion, understanding the categories of polygons is essential in geometry. It helps in identifying and classifying polygons based on their sides and angles. Regular vs Irregular and Simple vs Complex are the two main categories of polygons.
Counting The Sides
When it comes to polygons, counting the sides is an essential step to understanding their shapes and properties. By knowing how many sides a polygon has, we can classify it and explore its unique characteristics. In this section, we will explore the different approaches, tools, and techniques that can be used to count the sides of a polygon.
The Simplest Approaches
Counting the sides of a polygon can be as straightforward as visually inspecting its shape and manually counting the lines. This method works well for simple polygons with clearly defined edges. For example, if you have a triangle, you can easily count the three sides by visually following the lines of the shape. Similarly, for a square, you can count the four sides in the same manner.
Another simple approach is to refer to the polygon’s name. Many polygons have names that indicate the number of sides they possess. For instance, a pentagon has five sides, a hexagon has six sides, and an octagon has eight sides. By identifying the polygon’s name, you can quickly determine the number of sides it has without any additional calculations.
Tools And Techniques
For more complex polygons or situations where visual inspection is not sufficient, there are various tools and techniques available to count the sides accurately. One common approach is to use a ruler or measuring tape to measure the length of each side. By carefully measuring and recording the lengths, you can then count the number of sides based on the measurements.
Additionally, mathematical formulas can be applied to determine the number of sides of certain types of polygons. For example, the formula for the sum of the interior angles of a polygon can be used to calculate the number of sides. By rearranging the formula and solving for the number of sides, you can find the answer.
Furthermore, computer software and online tools can assist in counting the sides of complex polygons. These tools often provide features like drawing and measuring tools that can help identify and count the sides accurately.
Polygons In Nature And Design
Polygons in nature and design exhibit various sides, with each polygon uniquely defined by its number of sides. From the three sides of a triangle to the countless sides of intricate designs, polygons play a crucial role in shaping our natural world and artistic creations.
Polygons are not just shapes we learn about in math class, they can be found all around us in nature and design. From the honeycomb pattern of a beehive to the hexagonal shape of a snowflake, polygons are prevalent in natural occurrences. But they also play a significant role in architecture and art. In this blog post, we will explore the fascinating world of polygons in nature and design, including their natural occurrences and their influence on architecture and art.
Natural Occurrences
Polygons can be found in many natural phenomena, from the spiral shape of a seashell to the six-pointed star shape of a snowflake. One of the most well-known examples of polygons in nature is the honeycomb pattern of a beehive. Bees use hexagonal shapes to construct their honeycombs because it is the most efficient use of space. The hexagonal shape allows for the most storage space with the least amount of materials used, making it the perfect shape for bees to build their hives. Another example of polygons in nature is the pentagon-shaped leaves of the Venus flytrap. This unique plant uses its pentagonal shape to trap insects and protect itself from predators. The pentagonal shape creates a perfect seal, trapping the insect inside the plant where it is digested.
Influence On Architecture And Art
Polygons have been used in architecture and art for centuries. One of the most famous examples of polygons in architecture is the dome of the Pantheon in Rome. The dome is made up of intersecting arches that create a series of polygons, including squares, triangles, and octagons. This design not only creates a visually stunning effect but also helps distribute the weight of the dome evenly. In art, polygons have been used to create intricate designs and patterns. Islamic art is known for its use of geometric shapes, including polygons. The use of polygons in Islamic art is not just for aesthetic purposes; it also has a spiritual significance. The repetition of geometric shapes is believed to represent the underlying unity of the universe. In conclusion, polygons are not just shapes we learn about in math class, but they are prevalent in nature and design. From the honeycomb pattern of a beehive to the dome of the Pantheon in Rome, polygons have played a significant role in shaping our world. Their unique properties and efficient use of space make them a popular choice in architecture and art.
Mathematical Formulas Related To Polygons
Mathematical formulas related to polygons are essential for understanding and solving problems related to these geometric shapes. From calculating their perimeter and area to determining the angles and diagonals, these formulas provide the foundation for working with polygons in mathematics and real-world applications.
Perimeter And Area
The perimeter of a polygon is the sum of the lengths of all its sides. For a regular polygon, the formula to calculate the perimeter is the product of the number of sides (n) and the length of each side (s): P = n s. On the other hand, the area of a polygon can be calculated using different formulas depending on the type of polygon. For example, the area of a regular polygon can be found using the formula: A = 0.5 n s apothem, where ‘n’ represents the number of sides, ‘s’ is the length of each side, and ‘apothem’ is the distance from the center to the midpoint of any side.
Angles And Diagonals
The sum of the interior angles of a polygon can be calculated using the formula: Sum of interior angles = (n – 2) 180°, where ‘n’ represents the number of sides. Additionally, the number of diagonals in a polygon can be determined using the formula: Number of diagonals = 0.5 n (n – 3), where ‘n’ denotes the number of sides.

Credit: www.flickr.com
Famous Polygons And Their Properties
When it comes to polygons, there are many fascinating shapes that have captured our attention throughout history. Each polygon has its own unique properties and characteristics that make it special. In this section, we will explore two famous polygons – the hexagon and the octagon – and delve into their versatility and elegance.
The Versatility Of The Hexagon
The hexagon is a polygon with six sides, and it is known for its remarkable versatility. This shape can be found in various natural and man-made objects, showcasing its adaptability in different contexts. Here are some interesting facts about the hexagon:
- The sum of all interior angles in a hexagon is 720 degrees.
- Hexagons are often found in beehives, where their shape allows for efficient use of space.
- In nature, honeycomb structures and the basalt columns of the Giant’s Causeway in Northern Ireland are examples of hexagonal formations.
- In geometry, hexagons have symmetrical properties, making them aesthetically pleasing and visually appealing.
With its six sides and symmetrical design, the hexagon continues to captivate us with its versatility and widespread presence in both the natural and man-made world.
The Elegance Of The Octagon
The octagon, a polygon with eight sides, exudes elegance and sophistication. Its eight equal sides and angles give it a balanced and harmonious appearance. Here are some fascinating facts about the octagon:
- The sum of all interior angles in an octagon is 1080 degrees.
- Octagonal shapes can be found in numerous architectural designs, such as the famous Octagon Room in the White House.
- In art and design, the octagon is often used to create visually striking patterns and motifs.
- The stop sign, with its octagonal shape, is a universally recognized symbol for drivers to come to a halt.
With its eight sides and balanced proportions, the octagon stands as a symbol of elegance and beauty. Its presence in various fields, from architecture to art, showcases its timeless appeal.
Polygons In Technology
Exploring the significance of polygons in technology unveils their versatile applications in various fields. Let’s delve into how polygons play a crucial role in technology.
3d Modeling And Design
Polygons are fundamental in 3D modeling for creating realistic shapes and structures.
Cryptographic Applications
In cryptography, polygons are utilized for secure data encryption and decryption.
Credit: americanboard.org
Challenging The Limits: Infinite Sides
Discover the fascinating world of polygons and their infinite sides in “Challenging the Limits: Infinite Sides. ” Uncover the answer to the age-old question: How many sides does a polygon really have? Embark on a journey of discovery and expand your understanding of geometric shapes.
Approaching The Circle
In the realm of geometry, polygons are multi-sided figures. Some polygons, however, challenge the conventional notion of finite sides.
Theoretical Implications And Practical Uses
The concept of infinite-sided polygons leads us to explore theoretical implications and practical applications in various fields.
Frequently Asked Questions
How Many Sides Does A Polygon Have?
A polygon can have a minimum of three sides and a maximum of infinite sides. The number of sides defines the type of polygon, such as a triangle with three sides, a quadrilateral with four sides, and so on.
What Is The Name Of A 10-sided Polygon?
A 10-sided polygon is called a decagon. It is a two-dimensional shape with ten straight sides. Each angle in a regular decagon measures 144 degrees, making it a fascinating geometric figure.
How Do You Calculate The Number Of Sides In A Polygon?
To find the number of sides in a polygon, use the formula: Sum of interior angles = (n-2) * 180 degrees, where n is the number of sides. Rearranging the formula gives the number of sides as (Sum of interior angles / 180) + 2.
Conclusion
Understanding the number of sides a polygon has is fundamental in geometry. The blog has provided valuable insights into the properties of polygons. With this knowledge, you can easily identify and classify polygons in various shapes and sizes. Embracing this understanding enhances your grasp of geometric concepts.

